Top 100 Interview Questions and Answers on Strength of Materials

Last Updated on October 11, 2025 by Admin

Are you ready to leap into the highly competitive world of materials and civil engineering? As a candidate for a position in this field, you’re expected to be well-versed in the concepts and techniques of Strength of Materials. To help you navigate the complex maze of interview questions and impress potential employers, we’ve compiled the “Top 100 Interview Questions and Answers on Strength of Materials” – your indispensable guide to acing that all-important interview! Download our Strength of Materials interview questions PDF to revise core concepts quickly before your next interview.

Advertisements

It’s perfect for a quick revision or as a study aid to brush up on your knowledge before an interview, viva, or exam. The guide also includes specific questions frequently asked in civil engineering interviews and provides practical examples to reinforce your understanding.

What is Strength of Materials?

Simple diagram showing how materials respond to tension, compression, bending, and torsion with stress and strain definitions — A clear visual showing how different forces—pull, push, bend, and twist—affect materials, helping readers understand the basics of Strength of Materials.

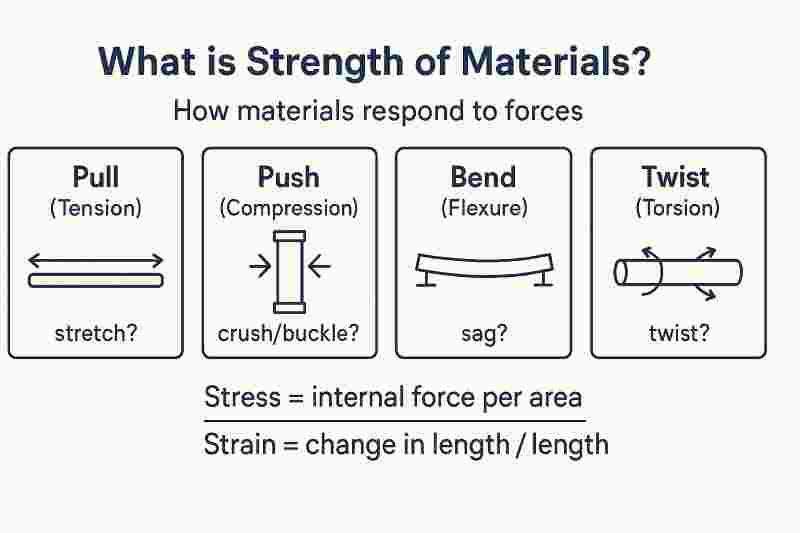
Strength of Materials (SoM)—also called Mechanics of Materials—is the study of how solid bodies respond to forces, moments, temperature, and constraints. It explains how internal stresses and strains develop inside a member and whether that member will deform, deflect, or fail. In practice, SoM helps engineers size beams and columns, choose materials, design shafts and pressure vessels, and check safety against yielding, fracture, buckling, and fatigue.

Why it matters

Ensures safety and serviceability of structures, machines, and components
Optimizes material usage and cost without compromising reliability
Builds intuition for failure modes so designs meet codes/standards

Core concepts at a glance

Stress–strain, Hooke’s law, modulus of elasticity, Poisson’s ratio
Axial loading, thermal stress, shear, and torsion (τ = T·r/J)
Bending and flexure (σ = M·y/I), combined stresses, Mohr’s circle
Deflection of beams (slope–deflection, area-moment), energy methods (Castigliano)
Stability and buckling (Euler column), failure theories (Max. shear, von Mises)

Typical applications

Civil: sizing RCC/steel beams, slabs, columns; checking deflection and crack control
Mechanical: designing drive shafts, keys, springs, fasteners, and pressure vessels
Manufacturing: material selection and QA based on allowable stresses/strain

Why Strength of Materials Interviews Matter in 2025

Are you ready to excel in today’s competitive materials engineering market?

Advertisements

Strength of materials remains a cornerstone of civil engineering and mechanical engineering interviews. In 2025, employers expect candidates to demonstrate both theoretical knowledge and practical application skills. Use the Strength of Materials Interview Questions PDF download section to get the complete set compiled by experts.

What Makes 2025 Different

Modern engineering interviews now emphasize:

Sustainability Integration: Understanding eco-friendly materials and sustainable building materials and techniques
Digital Simulation: Familiarity with FEA software and digital twins
Smart Materials: Knowledge of shape-memory alloys and self-healing concrete
AI-Driven Testing: Experience with automated testing and data analysis

Quick Stat: According to recent industry surveys, the global nanomaterials market, valued at USD 22.6 billion in 2024, is expected to grow at a CAGR of 14.3% from 2025 to 2035, making advanced materials knowledge crucial for career advancement. This guide also covers Strength of Materials Interview Questions mechanical for manufacturing, design, and production roles.

Essential Concepts Every Engineer Must Know

Before diving into specific questions, ensure you understand these fundamental principles:

Core Mechanical Properties

Stress = Force/Area (measured in Pascals or PSI)
Strain = Change in length/Original length (dimensionless)
Young’s Modulus = Stress/Strain (within elastic limit)

Key Material Behaviors

Elastic Deformation: Reversible shape change
Plastic Deformation: Permanent shape change
Failure Modes: Brittle vs. ductile fracture
Fatigue: Failure under cyclic loading

100 Interview Questions and Answers on the Strength of Materials

This comprehensive guide will delve into the most commonly asked questions during Strength of Materials interviews, complete with detailed answers and practical examples. If you’re new to the subject, start with Strength of materials Interview Questions for freshers to build confidence.

Whether you’re an aspiring materials engineer or a seasoned professional looking to improve your knowledge, this blog post covers you.

Advertisements

Prepare to explore the depths of key topics such as stress analysis, deformation, material properties, and failure theories. Through our easy-to-understand explanations and valuable insights, you’ll gain the confidence to tackle any interview question easily. You can also print the Strength of Materials Important Questions and Answers PDF for a quick offline cheat sheet.

Are you gearing up for an interview in the field of materials engineering or civil engineering? Look no further! Our “Top 100 Strength of Materials Questions and Answers” is the ultimate resource to help you prepare effectively. This comprehensive guide, available as a PDF, covers essential topics such as material properties, stress analysis, and failure theories.

Below, explore Strength of Materials interview questions and answers with step-by-step explanations and solved examples. So, buckle up and get ready to embark on a journey that will transform your approach to Strength of Materials interviews and help you land that dream job!

1. What is the Strength of Materials?
Answer: Strength of Materials (SOM) is a fundamental branch of Civil, Mechanical, and Structural Engineering that deals with the behavior of solid bodies under various types of loading such as tension, compression, torsion, and bending. It studies how materials resist deformation and failure when subjected to external forces.

2. What is Stress?
Answer: Stress (σ) is the internal resistance per unit area developed within a material when subjected to an external force.

$σ = A F$

Where:

Advertisements

σ = Stress
F = Applied Force
A = Cross-sectional Area

Stress helps engineers determine how much load a material can safely carry without failure.

3. What is Strain?
Answer: Strain (ε) is the deformation per unit original length of a material caused by applied stress.

$ε = L Δ L$

Where:

ε = Strain (dimensionless)
ΔL = Change in Length
L = Original Length

Strain measures the extent of deformation a material undergoes when stressed.

4. What is Hooke’s Law?
Answer: Hooke’s Law states that the strain produced in a material is directly proportional to the applied stress, provided the material remains within its elastic limit.

$σ = Eε$

Where:

E = Modulus of Elasticity (Young’s Modulus)
σ = Stress
ε = Strain

This law forms the basis for linear elasticity and is widely used in structural analysis and design.

5. What is the Modulus of Elasticity?
Answer: The Modulus of Elasticity (E) is defined as the ratio of stress to strain within the elastic limit of a material.

$E = ε σ$

It represents the stiffness of a material — the higher the value of E, the more resistant the material is to deformation under load.

Advertisements

Related Posts:

6. What is Poisson’s Ratio?

Poisson’s Ratio is the ratio of lateral strain to the corresponding longitudinal strain in a material under a tensile load.

7. What is Shear Stress?

Shear Stress is the internal resistance a material develops to a shear force.

8. What is Shear Strain?
Answer: Shear Strain (γ) is defined as the angular deformation per unit length of a material when subjected to a shear force. It represents the change in shape (distortion) without a volume change.

$γ = h Δ x$

Where:

γ = Shear Strain (in radians)
Δx = Lateral Displacement
h = Distance between the fixed and displaced planes

In simple terms, shear strain measures the angular distortion that occurs when one layer of a material slides over another.

9. What is Bending Moment?
Answer: The Bending Moment (M) at a section of a beam is the algebraic sum of all moments of the forces acting on one side of that section about the neutral axis. It determines the bending effect experienced by a beam under external loads.

A positive bending moment causes sagging (concave upward), while a negative bending moment causes hogging (concave downward).

10. What is the formula for Bending Moment?
Answer: The formula for Bending Moment is:

$M = F \times d$

Where:

M = Bending Moment
F = Force applied
d = Perpendicular distance from the line of action of the force to the neutral axis

This formula helps engineers determine the internal bending effect at any section of a beam due to external loads.

download pdf copy

11. What is the formula for Shear Force?

The formula for Shear Force is:

$V = d x d M$

Where:

V = Shear Force
M = Bending Moment
x = Distance along the length of the beam

This formula shows that the shear force at any section of a beam is equal to the rate of change of bending moment with respect to the beam’s length.

12. What is the formula for Deflection?

The formula for Deflection of a simply supported beam under a uniformly distributed load (UDL) is:

$δ = 384 E I 5 W L ^{4}$

Where:

δ = Maximum Deflection
W = Load on the beam (Uniformly distributed load)
L = Length of the beam
E = Modulus of Elasticity of the material
I = Moment of Inertia of the beam’s cross-section

This equation indicates that deflection increases with the fourth power of the beam’s length and decreases with greater stiffness (EI).

13. What is the Moment of Inertia?

The Moment of Inertia (I) is defined as the resistance of a beam’s cross-section to bending or rotation about an axis. It represents how the cross-sectional area is distributed relative to the axis of bending.

A higher moment of inertia means greater resistance to bending, which helps maintain the structural rigidity of beams and other components.

14. What is the formula for the Moment of Inertia of a rectangular section?

The formula for the Moment of Inertia of a rectangular section is:

$I = 12 b h ^{3}$

Where:

I = Moment of Inertia
b = Breadth (width) of the section
h = Height (depth) of the section

This formula shows that the moment of inertia increases significantly with the cube of the height.

15. What is the formula for the Moment of Inertia of a circular section?

The formula for the Moment of Inertia of a circular section is:

$I = 64 π d ^{4}$

Where:

I = Moment of Inertia
π = Constant (approximately 3.1416)
d = Diameter of the circle

This formula indicates that the moment of inertia of a circular section depends on the fourth power of its diameter, meaning small changes in diameter can greatly affect stiffness.

Related Posts:

16. What is the formula for the Moment of Inertia of a Triangular Section?
The formula for the Moment of Inertia of a triangular section is:

$I = 36 b h ^{3}$

Where:

I = Moment of Inertia
b = Breadth (base width) of the section
h = Height of the section

This formula indicates that the moment of inertia for a triangular section depends on the cube of its height and directly on its base width.

17. What is the formula for the Moment of Inertia of a Semicircular Section?
The formula for the Moment of Inertia of a semicircular section is:

$I = 128 π d ^{4}$

Where:

I = Moment of Inertia
π = Constant (approximately 3.1416)
d = Diameter of the section

This shows that a semicircular section has half the moment of inertia of a full circular section because of its reduced area distribution.

18. What is the formula for Shear Stress in a Rectangular Section?
The formula for Shear Stress in a rectangular section is:

$τ = I b V Q$

Where:

τ = Shear Stress
V = Shear Force
Q = First Moment of Area about the neutral axis
I = Moment of Inertia of the section
b = Breadth (width) of the section

This equation is used to determine how shear force is distributed across a rectangular beam’s cross-section.

19. What is the formula for Shear Stress in a Circular Section?
The formula for Shear Stress in a circular section is:

$τ = π d ^{2} 4 V$

Where:

τ = Shear Stress
V = Shear Force
π = Constant (approximately 3.1416)
d = Diameter of the section

This formula shows that shear stress in a circular section is directly proportional to the applied shear force and inversely proportional to the cross-sectional area.

20. What is the formula for Shear Stress in a Triangular Section?
The formula for Shear Stress in a triangular section is:

$τ = 2 I h 3 V Q$

Where:

τ = Shear Stress
V = Shear Force
Q = First Moment of Area
I = Moment of Inertia
h = Height of the section

This formula helps calculate shear stress distribution in triangular beams, where stress is maximum at a certain distance from the base rather than at the neutral axis.

download pdf copy

21. What is the formula for Shear Stress in a Semicircular Section?
The formula for Shear Stress in a semicircular section is:

$τ = π d 2 V$

Where:

τ = Shear Stress
V = Shear Force
π = Constant (approximately 3.1416)
d = Diameter of the section

This formula shows that shear stress in a semicircular section is inversely proportional to its diameter and directly proportional to the applied shear force.

22. What is the formula for Torsional Shear Stress in a Circular Section?
The formula for Torsional Shear Stress in a circular section is:

$τ = J T c$

Where:

τ = Torsional Shear Stress
T = Applied Torque
c = Radius of the section
J = Polar Moment of Inertia

This equation helps determine the maximum shear stress produced due to twisting in circular shafts or members under torsion.

23. What is the formula for the Polar Moment of Inertia of a Circular Section?
The formula for the Polar Moment of Inertia of a circular section is:

$J = 32 π d ^{4}$

Where:

J = Polar Moment of Inertia
π = Constant (approximately 3.1416)
d = Diameter of the circular section
This parameter measures the resistance of a circular section to twisting or torsional deformation.

24. What is the formula for the Polar Moment of Inertia of a Rectangular Section?
The formula for the Polar Moment of Inertia of a rectangular section is:

$J = 3 b ^{3} h$

Where:

J = Polar Moment of Inertia
b = Breadth (width) of the section
h = Height (depth) of the section

This formula is used to determine the torsional rigidity of rectangular members subjected to twisting.

25. What is the formula for the Polar Moment of Inertia of a Triangular Section?
The formula for the Polar Moment of Inertia of a triangular section is:

$J = 16 b h ^{3}$

Where:

J = Polar Moment of Inertia
b = Breadth (base width) of the section
h = Height of the section

This shows that the torsional resistance of a triangular section depends significantly on its height, as it varies with the cube of $h$ .

Related Posts:

26. What is the formula for the Polar Moment of Inertia of a Semicircular Section?
The formula for the Polar Moment of Inertia of a semicircular section is:

$J = 64 π d ^{4}$

Where:

J = Polar Moment of Inertia
π = Constant (approximately 3.1416)
d = Diameter of the section

This formula indicates the torsional resistance of a semicircular section, which is half of that of a full circular section due to its reduced geometry.

27. What is the formula for Maximum Bending Stress?
The formula for Maximum Bending Stress is:

$σ_{ma x} = I M c$

Where:

σmax = Maximum Bending Stress
M = Bending Moment
c = Distance from the neutral axis to the outermost fiber
I = Moment of Inertia

This formula helps determine the maximum stress experienced at the extreme fiber of a beam when subjected to bending.

28. What is the formula for the Neutral Axis?
The formula for locating the Neutral Axis is:

$y = A I x$

Where:

y = Distance from the neutral axis
I = Moment of Inertia
x = Distance from the extreme fiber
A = Cross-sectional Area

The neutral axis is the line in the beam’s cross-section where the bending stress is zero — it separates the compression and tension zones.

29. What is the formula for Maximum Deflection?
The formula for Maximum Deflection of a simply supported beam under a concentrated load is:

$δ_{ma x} = 48 E I W L ^{3}$

Where:

δmax = Maximum Deflection
W = Load applied
L = Length of the beam
E = Modulus of Elasticity of the material
I = Moment of Inertia of the cross-section

This equation shows that deflection increases with the cube of the beam’s length and decreases with higher stiffness (EI).

30. What is the difference between Axial Load and Eccentric Load?

Axial Load: A load applied through the centroid of a section, producing only direct stress without bending.
Eccentric Load: A load applied away from the centroid, causing both direct stress and bending stress due to the moment created by eccentricity.

In simple terms, axial loads create pure compression or tension, whereas eccentric loads cause combined bending and compression/tension.

download pdf copy

31. What is the difference between Direct Stress and Bending Stress?

Direct Stress: It is the stress developed in a member due to an axial load acting along its length. This type of stress is uniform across the cross-section and does not cause bending.
Bending Stress: It is the stress developed in a member due to a bending moment. It varies linearly across the section — compressive on one side and tensile on the other.

In short, direct stress results from axial forces, while bending stress results from bending moments.

32. What is the difference between Compressive Stress and Tensile Stress?

Compressive Stress: Occurs when a material is subjected to compression, i.e., forces act toward each other, reducing the length of the material.
Tensile Stress: Occurs when a material is subjected to tension, i.e., forces act away from each other, increasing the length of the material.

Compressive stress tends to shorten a material, while tensile stress tends to elongate it.

33. What is the difference between Shear Stress and Bearing Stress?

Shear Stress: It is the stress developed in a material when it is subjected to a shear force that tries to make one layer slide over another.
Bearing Stress: It is the stress developed when a material is subjected to compressive force over a contact area, such as between a bolt and a plate.

In essence, shear stress acts parallel to the surface, while bearing stress acts perpendicular to the surface.

34. What is the difference between Pure Bending and Shear Bending?

Pure Bending: Occurs when a beam is subjected only to a constant bending moment with no shear force acting along its length.
Shear Bending: Occurs when a beam experiences both bending moment and shear force, leading to combined stresses and deflection.

Thus, pure bending results in uniform curvature, whereas shear bending involves both curvature and shear deformation.

35. What is the difference between Moment of Inertia and Polar Moment of Inertia?

Moment of Inertia (I): A geometric property that measures a section’s resistance to bending about a given axis. It applies primarily to beams and flexural members.
Polar Moment of Inertia (J): A property that measures a section’s resistance to torsion (twisting) about a central axis. It applies mainly to circular shafts.

In summary, Moment of Inertia deals with bending stiffness, while Polar Moment of Inertia deals with torsional stiffness.

Related Posts:

36. What is the difference between Elastic Limit and Yield Point?

Elastic Limit: The maximum stress that a material can withstand without any permanent deformation. Beyond this limit, the material will not return to its original shape when the load is removed.
Yield Point: The stress level at which a material begins to deform plastically, meaning it will no longer return to its original shape even after the removal of the load.

In summary, the elastic limit marks the end of purely elastic behavior, while the yield point marks the beginning of plastic deformation.

37. What is the difference between Ductility and Brittleness?

Ductility: The ability of a material to undergo significant plastic deformation before fracturing. Ductile materials can be drawn into wires or elongated without breaking (e.g., steel, copper).
Brittleness: The tendency of a material to fracture with little or no plastic deformation when subjected to stress (e.g., cast iron, glass).

Thus, ductile materials absorb more energy before failure, while brittle materials fail suddenly without warning.

38. What is the difference between Elastic Modulus and Rigidity Modulus?

Elastic Modulus (Young’s Modulus): A measure of a material’s stiffness under axial (tensile or compressive) loading. It defines the ratio of stress to strain in the linear elastic region.
$E = Strain Stress$
Rigidity Modulus (Shear Modulus): A measure of a material’s stiffness under shear loading. It defines the ratio of shear stress to shear strain.
$G = Shear Strain Shear Stress$

In short, Elastic Modulus relates to tensile stiffness, while Rigidity Modulus relates to shear stiffness.

39. What is the difference between the Shear Center and the Center of Gravity?

Shear Center: The point in a beam’s cross-section where shear forces can act without causing twisting or torsion. It depends on the geometry of the section.
Center of Gravity: The point where the entire weight of the body or section can be considered to act. It represents the average position of the body’s mass.

In summary, the shear center deals with force application and torsion, while the center of gravity deals with mass distribution.

40. What is the difference between Stress and Strain?

Stress: The internal resistance per unit area developed within a material when subjected to an external force.
$σ = A F$
Strain: The deformation per unit length of a material when subjected to stress.
$ε = L δ L$

In short, stress represents the cause (force per area), while strain represents the effect (deformation per length).

download pdf copy

41. What is the difference between Normal Stress and Shear Stress?

Normal Stress: It is the stress developed perpendicular to the plane of a section when a material is subjected to an axial load.
Shear Stress: It is the stress developed parallel to the plane of a section when a material is subjected to a shear force.

In short, normal stress acts normal (⊥) to the surface, while shear stress acts tangentially (∥) to it.

42. What is the difference between Bending Stress and Torsional Stress?

Bending Stress: A stress developed in a material due to bending moment, resulting in compression on one side and tension on the other.
Torsional Stress: A stress developed in a material due to twisting or torque, producing shear stress throughout the cross-section.

Thus, bending stress is caused by flexural loads, while torsional stress is caused by rotational loads.

43. What is the difference between Longitudinal Strain and Lateral Strain?

Longitudinal Strain: The strain that occurs along the length of a material when subjected to axial loading.
$ε_{L} = L Δ L$
Lateral Strain: The strain that occurs perpendicular to the length (width or thickness) due to the same axial load.
$ε_{T} = D Δ D$

When a material is stretched, it elongates longitudinally and contracts laterally — these two strains are related through Poisson’s ratio.

44. What is the difference between Creep and Fatigue?

Creep: The gradual, time-dependent deformation of a material under a constant load over a long period, typically at high temperature.
Fatigue: The progressive failure of a material due to repeated or cyclic loading, even at stress levels below its yield strength.

In summary, creep occurs under sustained loading, while fatigue occurs under cyclic loading.

45. What is the difference between Ultimate Strength and Yield Strength?

Ultimate Strength: The maximum stress that a material can withstand before fracture or failure occurs.
Yield Strength: The stress level at which a material begins to deform plastically, losing its ability to return to the original shape.

In short, yield strength marks the start of permanent deformation, while ultimate strength marks the maximum load-bearing capacity.

46. What is the difference between Modulus of Elasticity and Modulus of Rigidity?

Modulus of Elasticity (E): It measures a material’s stiffness under axial loading (tension or compression).
$E = Strain Stress$
Modulus of Rigidity (G): It measures a material’s stiffness under shear loading.
$G = Shear Strain Shear Stress$

Thus, E applies to axial deformation, while G applies to shear deformation.

47. What is the difference between Homogeneous and Composite Materials?

Homogeneous Materials: Materials having uniform composition and properties throughout (e.g., steel, copper, aluminum).
Composite Materials: Materials made up of two or more constituents with different properties combined to achieve improved performance (e.g., reinforced concrete, carbon fiber).

In summary, homogeneous materials are single-phase, while composite materials are multi-phase.

48. What is the difference between Isotropic and Anisotropic Materials?

Isotropic Materials: Materials having identical mechanical properties in all directions (e.g., mild steel, glass).
Anisotropic Materials: Materials having different properties in different directions (e.g., wood, composites).

Hence, isotropic materials exhibit uniform behavior, while anisotropic materials exhibit direction-dependent behavior.

49. What is the difference between Steel and Concrete?

Steel: A strong, ductile, and flexible material capable of withstanding high tensile and compressive stresses. Commonly used for reinforcement and structural framing.
Concrete: A hard, durable, and brittle material primarily strong in compression but weak in tension. Commonly used for foundations, slabs, and compression members.

In reinforced concrete, steel and concrete complement each other, combining tensile and compressive strength.

50. What is the difference between Compression and Tension Members?

Compression Members: Structural elements that carry axial compressive forces, tending to shorten the member (e.g., columns, struts).
Tension Members: Structural elements that carry axial tensile forces, tending to elongate the member (e.g., tie rods, trusses).

Thus, compression members resist buckling, while tension members resist stretching.

Related Posts:

51. What is the difference between Beams and Columns?

Beams are structural members that are designed to carry bending loads, whereas Columns are structural members that are designed to carry compressive loads.

download pdf copy

52. What is the difference between Shear Wall and Retaining Wall?

Shear Wall: A vertical structural element designed to resist lateral loads such as wind, earthquake, and seismic forces acting on a building. It enhances stiffness and prevents excessive sway.
Retaining Wall: A structure built to retain or hold back soil, water, or other materials, preventing lateral movement or erosion of earth.

In summary, shear walls resist lateral loads on buildings, while retaining walls resist lateral earth pressure.

53. What is the difference between Reinforced Concrete and Prestressed Concrete?

Reinforced Concrete (RCC): Concrete that is strengthened with steel bars or mesh to improve its tensile and ductile capacity. The steel takes tensile stresses while the concrete takes compressive stresses.
Prestressed Concrete (PSC): Concrete in which compressive stresses are intentionally introduced before applying external loads, typically using high-tensile steel tendons.

Thus, RCC resists tension through reinforcement, while PSC resists tension by pre-inducing compression.

54. What is the difference between Simple Stresses and Compound Stresses?

Simple Stresses: Developed when a material is subjected to a single type of force, such as tension, compression, or shear acting alone.
Compound Stresses: Developed when a material is subjected to two or more types of stresses simultaneously, such as combined bending and torsion.

In short, simple stresses involve one type of loading, while compound stresses involve multiple loadings acting together.

55. What is the difference between Moment of Resistance and Section Modulus?

Moment of Resistance (Mₐ): The maximum bending moment that a section can resist without failure. It depends on the material strength and section geometry.
Section Modulus (Z): A geometrical property of a section, given by:
$Z = c I$
where I = Moment of Inertia, and c = Distance from the neutral axis to the outermost fiber.

In simple terms, Section Modulus indicates strength potential, while Moment of Resistance indicates actual strength capacity.

56. What is the difference between Live Load and Dead Load?

Live Load: A temporary or variable load that changes over time, such as occupants, furniture, or vehicles.
Dead Load: A permanent and constant load that includes the self-weight of structural elements and fixed installations.

Thus, live loads are movable and dynamic, whereas dead loads are permanent and static.

57. What is the difference between Stress Concentration and Stress Corrosion?

Stress Concentration: A localized increase in stress at points of abrupt change in geometry, such as holes, notches, or sharp corners.
Stress Corrosion: The gradual degradation or cracking of a material due to the combined effect of tensile stress and corrosive environment.

In summary, stress concentration is a mechanical phenomenon, while stress corrosion is a chemical–mechanical phenomenon.

58. What is the difference between Resilience and Toughness?

Resilience: The ability of a material to absorb energy within the elastic limit and recover its original shape after unloading.
Toughness: The ability of a material to absorb total energy (elastic + plastic) before fracturing.

Hence, resilience measures elastic energy absorption, while toughness measures total energy absorption up to failure.

59. What is the difference between Elongation and Extension?

Elongation: The increase in length of a material under tensile stress, usually expressed as a percentage of the original length.
Extension: The total deformation or change in length of a material when subjected to any external force (tension, compression, or bending).

Thus, elongation is a specific case of extension under tensile loading.

60. What is the difference between Fatigue Limit and Endurance Limit?

Fatigue Limit: The maximum stress amplitude that a material can endure indefinitely (infinite cycles) without failure.
Endurance Limit: The maximum stress amplitude a material can sustain for a finite number of cycles before failure.

In short, the fatigue limit refers to infinite life, while the endurance limit refers to finite life under cyclic loading.

Related Posts:

61. What is the difference between Damping and Stiffness?

Damping: The ability of a material or system to dissipate energy when subjected to cyclic or vibratory loading. It helps in reducing oscillations and controlling vibrations.
Stiffness: The ability of a material to resist deformation under applied external forces. It defines how much force is required to cause a given displacement.

In short, damping controls motion by energy dissipation, while stiffness controls motion by resistance to deformation.

Download PDF Copy

62. What is the difference between Flexure and Shear?

Flexure: Refers to the bending of a structural member when subjected to a transverse load. The stress developed due to flexure is known as bending stress.
Shear: Refers to the sliding or shifting of adjacent layers within a material when subjected to parallel or tangential forces. The stress developed is known as shear stress.

Thus, flexure causes bending, while shear causes sliding deformation within the material.

63. What is the difference between Yield Point and Plastic Range?

Yield Point: The specific stress value at which a material begins to deform plastically and no longer returns to its original shape when unloaded.
Plastic Range: The range of stresses beyond the yield point within which the material undergoes plastic (permanent) deformation before fracture.

In short, the yield point marks the beginning, and the plastic range defines the extent of plastic deformation.

64. What is the difference between Fracture and Failure?

Fracture: The breaking or cracking of a material into two or more parts under excessive stress.
Failure: The inability of a material or structure to perform its intended function, which may occur due to fracture, excessive deformation, or instability.

Hence, fracture is a type of failure, but failure can occur without fracture.

65. What is the difference between Buckling and Bending?

Buckling: The sudden lateral or torsional deformation of a slender column or member due to compressive forces, leading to instability.
Bending: The gradual deformation of a beam or member under transverse loading that produces curvature.

Thus, buckling is an instability failure caused by compression, while bending is an elastic deformation due to external moments.

66. What is the difference between Fatigue Crack and Stress Corrosion Crack?

Fatigue Crack: A progressive crack formed due to repeated cyclic loading even at stress levels below the material’s yield strength.
Stress Corrosion Crack: A crack induced by the combined effect of tensile stress and a corrosive environment, typically leading to sudden brittle failure.

In essence, fatigue cracking is caused by cyclic stress, while stress corrosion cracking is caused by stress + corrosion.

67. What is the difference between Shear Center and Center of Twist?

Shear Center: The point in a cross-section where applied shear forces do not cause torsion. It depends on the shape and geometry of the section.
Center of Twist: The point in a section where applied torsion produces no resultant shear force, causing pure twisting.

In simple terms, the shear center relates to shear force equilibrium, while the center of twist relates to torsional equilibrium.

68. What is the difference between Strain Energy and Residual Stress?

Strain Energy: The energy stored in a material when it is deformed under the action of external forces. It is recoverable if the material returns to its original shape.
Residual Stress: The internal stress remaining in a material after the external forces are removed, often due to uneven cooling, welding, or plastic deformation.

Hence, strain energy represents temporary stored energy, while residual stress represents permanent locked-in stress.

69. What is the difference between Resilience and Modulus of Resilience?

Resilience: The ability of a material to absorb energy within the elastic limit and recover its shape after unloading.
Modulus of Resilience: The amount of energy per unit volume that can be absorbed without permanent deformation. It is given by:
$U_{r} = 2 E σ ^{y 2}$
where σᵧ = Yield Stress and E = Modulus of Elasticity.

Thus, resilience is a qualitative property, while modulus of resilience is a quantitative measure of it.

70. What is the difference between Principal Stress and Maximum Shear Stress?

Principal Stress: The maximum and minimum normal stresses that act on mutually perpendicular planes where shear stress is zero.
Maximum Shear Stress: The greatest value of shear stress acting on a plane inclined at 45° to the principal stress planes.

In short, principal stress defines normal stress extremes, while maximum shear stress defines shear stress extremes in a material.

download pdf copy

71. What is the difference between Ductile Materials and Brittle Materials?

Ductile Materials: These materials can undergo significant plastic deformation before failure. They exhibit warning signs before fracture, such as elongation or necking. (Examples: Mild steel, copper, aluminum)
Brittle Materials: These materials fail suddenly without noticeable plastic deformation and absorb very little energy before fracture. (Examples: Cast iron, glass, concrete)

In short, ductile materials deform before breaking, while brittle materials fracture suddenly.

72. What is the difference between Hardness and Toughness?

Hardness: The resistance of a material to penetration, indentation, or scratching. It indicates surface strength and wear resistance.
Toughness: The ability of a material to absorb energy and withstand shock or impact before fracturing.

Hence, hardness measures surface resistance, whereas toughness measures total energy absorption before failure.

73. What is the difference between Hooke’s Law and Poisson’s Ratio?

Hooke’s Law: States that stress is directly proportional to strain within the elastic limit of a material.
$σ = E \times ε$
where σ = Stress, E = Modulus of Elasticity, ε = Strain.
Poisson’s Ratio: Defines the ratio of lateral strain to longitudinal strain in a material subjected to axial stress.
$μ = Longitudinal Strain Lateral Strain$

In short, Hooke’s Law relates stress and strain, while Poisson’s Ratio relates two perpendicular strains.

74. What is the difference between Deflection and Slope?

Deflection: The vertical or lateral displacement of a beam or structural element from its original position due to applied loads.
Slope: The angular change or inclination of the deflected shape of the beam at a specific point, representing the tangent angle to the deflection curve.

Thus, deflection measures displacement, while slope measures angular deviation.

75. What is the difference between Section Modulus and Radius of Gyration?

Section Modulus (Z): A geometrical property used to measure a section’s bending strength, defined as:
$Z = c I$
where I = Moment of Inertia and c = Distance from the neutral axis to the outermost fiber.
Radius of Gyration (k): A geometrical property indicating how the area is distributed about the centroidal axis, defined as:
$k = A I$
where I = Moment of Inertia and A = Area of the section.

In summary, Section Modulus relates to bending strength, while Radius of Gyration relates to buckling stability.

Related Posts:

76. What is the difference between Elastic Limit and Proportional Limit?

Elastic Limit: The maximum stress that a material can withstand without permanent deformation. Beyond this limit, the material will not return to its original shape when the load is removed.
Proportional Limit: The maximum stress up to which stress and strain remain directly proportional, obeying Hooke’s Law.

In summary, the proportional limit marks the end of linear elasticity, while the elastic limit marks the end of recoverable deformation.

77. What is the difference between Shear Force and Bending Moment?

Shear Force (V): The internal force that acts parallel to the cross-section of a beam and tends to slide one layer over another.
Bending Moment (M): The moment of internal forces that tends to bend the beam about an axis.

In short, shear force causes sliding deformation, whereas bending moment causes rotational or flexural deformation in a beam.

78. What is the difference between Yield Strength and Ultimate Strength?

Yield Strength: The stress level at which a material begins to deform plastically and can no longer return to its original shape when unloaded.
Ultimate Strength: The maximum stress that a material can withstand before fracture or failure occurs.

Thus, yield strength indicates the onset of permanent deformation, while ultimate strength defines the maximum load-bearing capacity.

79. What is the difference between Dynamic Load and Static Load?

Dynamic Load: A time-varying load that changes in magnitude, direction, or position with time — such as impact, wind, or seismic loads.
Static Load: A constant or slowly varying load that remains uniform over time — such as dead loads or permanent weights.

In simple terms, dynamic loads involve motion and acceleration, whereas static loads are steady and constant.

80. What is the difference between Buckling and Yielding?

Buckling: A sudden instability or lateral deformation of a slender member under compressive stress, leading to failure even below the yield strength.
Yielding: A gradual plastic deformation of a material when stress exceeds the yield strength, occurring without loss of stability.

Hence, buckling is a stability failure due to compression, while yielding is a material failure due to exceeding strength limits.

download pdf copy

81. What is the difference between Stress and Pressure?

Stress: The internal resistance developed within a material when subjected to an external force. It acts internally over a cross-sectional area.
$Stress (σ) = A F$
Pressure: The external force per unit area applied uniformly on a surface by a fluid or another medium.
$Pressure (P) = A F$

Although both have the same units (N/m² or Pa), stress is internal and directional, while pressure is external and acts equally in all directions.

82. What is the difference between Load and Stress?

Load: The external force or weight applied to a structure or material (e.g., tension, compression, or shear).
Stress: The internal resistance per unit area developed within the structure in response to the applied load.

In summary, load is the cause, while stress is the effect produced within the material.

83. What is the difference between Elastic Deformation and Plastic Deformation?

Elastic Deformation: The temporary deformation of a material that is completely recovered when the external force is removed.
Plastic Deformation: The permanent deformation that remains even after the external load is removed, occurring beyond the material’s yield point.

Thus, elastic deformation is reversible, whereas plastic deformation is irreversible.

84. What is the difference between Bending Stresses and Axial Stresses?

Bending Stresses: Developed in a member due to bending moment, varying linearly across the section — compression on one side and tension on the other.
Axial Stresses: Developed due to axial loading (tensile or compressive), and are uniformly distributed across the cross-section.

In essence, bending stresses vary across the section, while axial stresses remain uniform.

85. What is the difference between Shear Center and Elastic Center?

Shear Center: The point in a cross-section where shear forces can act without causing torsion or twisting. It depends solely on the geometry of the section.
Elastic Center: The point in a section where loads can be applied without causing deformation (translation or rotation). It depends on both geometry and material distribution.

In short, the shear center concerns shear equilibrium, while the elastic center concerns overall deformation balance.

86. What is the difference between Reinforcement and Stirrups?

Reinforcement: Refers to the main longitudinal steel bars placed within concrete to improve its tensile strength, ductility, and load-carrying capacity. These bars resist bending and tensile forces.
Stirrups: Are closed-loop steel bars or ties provided transversely around the main reinforcement to resist shear forces and hold the main bars in position.

In summary, reinforcement bars resist bending and tension, while stirrups resist shear and prevent cracking or buckling.

87. What is the difference between Elastic Constants and Strength Constants?

Elastic Constants: The material properties that define the relationship between stress and strain within the elastic limit (e.g., Young’s modulus, shear modulus, bulk modulus, and Poisson’s ratio).
Strength Constants: The parameters that represent the maximum stress a material can endure before failure (e.g., yield strength, ultimate tensile strength, and compressive strength).

Thus, elastic constants describe deformation behavior, while strength constants describe failure behavior.

88. What is the difference between Torsion and Shear?

Torsion: The twisting of a structural member about its longitudinal axis due to an external torque or moment, generating shear stresses over the cross-section.
Shear: The sliding of adjacent layers of a material parallel to each other under the action of a transverse force.

In simple terms, torsion is twisting caused by moments, while shear is sliding caused by forces.

89. What is the difference between Neutral Axis and Centroid?

Neutral Axis: The axis within a cross-section where the bending stress is zero when a member is subjected to bending or axial loading.
Centroid: The geometrical center of a cross-section, where the entire area can be assumed to be concentrated for analysis.

In general, for symmetric and homogeneous sections under pure bending, the neutral axis passes through the centroid.

90. What is the difference between Design Load and Service Load?

Design Load: The factored load used in structural design, obtained by multiplying the actual load by a load factor to ensure safety and reliability.
$Design Load = Service Load \times Load Factor$
Service Load: The actual load experienced by a structure during normal use, such as dead load, live load, and environmental loads.

In short, service load is the real load, while design load is the safe load used for design calculations.

91. What is the difference between Strain Hardening and Strain Softening?

Strain Hardening (Work Hardening): The phenomenon where a material becomes stronger and harder when subjected to plastic deformation. This occurs due to dislocation interactions that increase resistance to further deformation.
Strain Softening: The phenomenon where a material becomes weaker and less ductile after deformation, often due to micro-crack formation or material degradation.

In summary, strain hardening improves strength, while strain softening reduces strength after deformation.

92. What is the difference between Statically Determinate and Statically Indeterminate Structures?

Statically Determinate Structures: Structures that can be completely analyzed using only the equations of static equilibrium (ΣF = 0 and ΣM = 0). Internal forces and reactions are found without considering deformation.
Statically Indeterminate Structures: Structures that cannot be solved using equilibrium equations alone and require compatibility and deformation equations for analysis.

Thus, determinate structures depend solely on equilibrium, while indeterminate structures depend on both equilibrium and material deformation conditions.

93. What is the difference between Linear Elasticity and Nonlinear Elasticity?

Linear Elasticity: A behavior where stress is directly proportional to strain, following Hooke’s Law. The material returns to its original shape upon unloading.
$σ = Eε$
Nonlinear Elasticity: A behavior where stress is not proportional to strain, even though the deformation may still be recoverable upon unloading.

In essence, linear elasticity shows a straight-line stress-strain curve, while nonlinear elasticity shows a curved relationship.

94. What is the difference between Tension and Compression?

Tension: A pulling or stretching force that increases the length of a material, developing tensile stress.
Compression: A pushing or squeezing force that reduces the length of a material, developing compressive stress.

Thus, tension elongates a member, while compression shortens it.

95. What is the difference between Dead Load and Live Load?

Dead Load: The permanent and constant load on a structure due to its self-weight and fixed components, such as beams, walls, and slabs.
Live Load: The temporary and variable load acting on a structure, such as people, furniture, and vehicles.

In short, dead load remains constant, while live load varies over time.

Related Posts:

96. What is the difference between Working Stress and Allowable Stress?

Working Stress: The actual stress used in the design of a structural member, obtained by dividing the applied load by the cross-sectional area. It represents the expected stress under service conditions.
Allowable Stress: The maximum safe stress that a material can withstand without failure, usually determined by applying a factor of safety (F.S.) to the material’s yield or ultimate strength.
$Allowable Stress = Factor of Safety Yield or Ultimate Stress$

In short, working stress is the actual stress in service, while allowable stress is the permissible design limit.

97. What is the difference between Principal Planes and Principal Stresses?

Principal Planes: The planes within a stressed body where shear stress is zero and only normal stresses act.
Principal Stresses: The maximum and minimum normal stresses acting on the principal planes, oriented at right angles to each other.

Hence, principal planes define orientation, while principal stresses define magnitude of the maximum and minimum normal stresses.

98. What is the difference between Yield Point and Ultimate Point?

Yield Point: The stress level at which a material begins to deform plastically and does not return to its original shape upon unloading.
Ultimate Point: The maximum stress a material can withstand before fracture or failure occurs.

Thus, yield point indicates the onset of plastic deformation, while ultimate point indicates the peak strength before rupture.

99. What is the difference between Flexural Rigidity and Torsional Rigidity?

Flexural Rigidity (EI): The measure of resistance to bending of a beam, given by the product of Modulus of Elasticity (E) and Moment of Inertia (I).
$Flexural Rigidity = E \times I$
Torsional Rigidity (GJ): The measure of resistance to twisting of a shaft or member, given by the product of Modulus of Rigidity (G) and Polar Moment of Inertia (J).
$Torsional Rigidity = G \times J$

In essence, flexural rigidity resists bending deformation, while torsional rigidity resists twisting deformation.

100. What is the difference between Laminar and Isotropic Materials?

Laminar Materials: Materials that are layered or laminated, often exhibiting different properties in different directions (anisotropic behavior). Example: Plywood, composite laminates.
Isotropic Materials: Materials that have identical mechanical properties in all directions, exhibiting uniform behavior regardless of orientation. Example: Steel, aluminum, glass.

In short, laminar materials are direction-dependent, while isotropic materials are direction-independent.

download pdf copy

Additional Questions & Updated Answers

Below are 10 sample questions (from the comprehensive list of 100) that have been revised to reflect current trends and standards. For a full list, please refer to our updated downloadable PDF.

Advanced Strength of Materials Interview Questions (Q101–Q110)

101. What is the significance of the Modulus of Elasticity in modern engineering applications?
Answer: The Modulus of Elasticity (E) defines a material’s stiffness—its ability to resist deformation under load. It is essential in designing structures that must endure dynamic and fluctuating loads. In modern engineering, digital simulation tools such as Finite Element Analysis (FEA) are used to model stress-strain behavior accurately, improving the efficiency, reliability, and safety of structural designs.

102. How do you determine the Yield Strength of a material, and why is it important?
Answer: Yield strength is determined through standard tensile testing, where a material sample is subjected to increasing stress until plastic deformation begins. It is a key design parameter, indicating the limit beyond which permanent deformation occurs. With the integration of digital sensors and automated testing systems, yield strength measurement has become more precise and data-driven, enhancing quality control in modern manufacturing and construction.

103. Can you explain the concept of Fatigue in materials with an example from recent projects?
Answer: Fatigue is the progressive weakening of a material caused by repeated cyclic loading. For example, in modern bridge engineering, embedded smart sensors collect real-time data on stress cycles to monitor fatigue performance. This data enables predictive maintenance, extending the lifespan and safety of critical infrastructure.

104. How have modern simulation tools changed the analysis of stress and strain in materials?
Answer: Advanced tools like Finite Element Analysis (FEA), ANSYS, and Abaqus have transformed stress-strain analysis by enabling virtual prototyping. Engineers can now model complex materials, simulate real-world conditions, and evaluate failure modes before physical construction—resulting in cost-efficient, sustainable, and optimized designs.

105. What new materials are influencing the field of Strength of Materials, and how are they tested?
Answer: Carbon fiber composites, high-performance polymers, and nano-engineered materials are redefining modern construction and manufacturing. These materials undergo non-destructive testing (NDT) methods such as ultrasonic inspection and digital image correlation (DIC) to assess structural integrity and ensure compliance with international performance and safety standards.

106. Describe the importance of Safety Factors in design and how modern engineering standards address them.
Answer: Safety factors provide a margin between actual stresses and failure limits to account for uncertainties in material properties and loading conditions. Modern design codes (such as Eurocode, AISC, and IS standards) now incorporate probabilistic safety analysis and real-time monitoring data, ensuring that structures can endure unforeseen or extreme conditions with higher confidence.

107. What role does Sustainability play in the selection of materials today?
Answer: Sustainability is a core criterion in modern material selection. Engineers now assess not only strength and cost but also environmental impact, recyclability, and embodied carbon. For example, green concrete, bamboo composites, and recycled steel are gaining popularity for their lower carbon footprint and long-term performance benefits.

108. How do recent advancements in material testing improve the reliability of engineering designs?
Answer: Modern testing methods use automation, robotics, and AI-powered data analysis to enhance accuracy and reproducibility. This minimizes human error and ensures consistent quality assurance, resulting in safer and more predictable engineering designs, particularly in aerospace, automotive, and civil infrastructure projects.

109. What are the common challenges engineers face when dealing with Composite Materials?
Answer: Key challenges include anisotropic behavior, difficult failure prediction, and variations in manufacturing quality. Engineers now leverage machine learning algorithms and computational modeling to predict the behavior of composites under complex loading conditions, leading to more precise and efficient designs.

110. How do you keep current with evolving standards and technologies in Strength of Materials?
Answer: Continuous professional learning is vital. Engineers stay updated by attending webinars, industry workshops, and certification programs, and by following leading journals such as the Journal of Materials Science, ASCE Materials Journal, and Elsevier’s Construction and Building Materials. Engaging with professional bodies like ASME, ACI, and IS 800 committees ensures alignment with the latest standards and innovations.

Modern Testing Standards and Methods

Key Organizations and Standards

ASTM International

ASTM International standards positively impact public health and safety, consumer confidence, and overall quality of life. Critical standards include:

ASTM E8/E8M: Standard Test Methods for Tension Testing of Metallic Materials
ASTM D638: Standard Test Method for Tensile Properties of Plastics
ASTM C39: Standard Test Method for Compressive Strength of Cylindrical Concrete Specimens

ASCE (American Society of Civil Engineers)

ASCE standards provide technical guidelines for civil engineering applications:

ASCE 7-22: Minimum Design Loads and Associated Criteria for Buildings and Other Structures
ASCE 24: Flood Resistant Design and Construction

Advanced Testing Methods

Digital Image Correlation (DIC): Non-contact method for measuring surface deformation Fiber Optic Sensing: Real-time strain monitoring in structures Automated Testing Systems: AI-driven testing protocols for consistent results.

We’ve curated Strength of materials interview questions civil engineering focused on RCC, steel design, and geotechnical basics.

Industry Trends and Emerging Technologies

Material Informatics

The material informatics market, valued at USD 154.78 million in 2024, is expected to grow from USD 179.92 million in 2025 to USD 705.21 million by 2034, with a CAGR of 16.4%. This field combines materials science with big data analytics to accelerate material discovery.

Additive Manufacturing Integration

3D printing technologies now produce materials with properties tailored for specific applications, requiring new testing methodologies and material characterization techniques.

Sustainable Materials Revolution

Engineers increasingly focus on:

Bio-based composites: Made from natural fibers and recyclable resins
Circular design principles: Materials designed for reuse and recycling
Low-carbon alternatives: Reducing embodied energy in material production

Interview Preparation Strategies

Technical Preparation

Review fundamental concepts: Ensure solid understanding of stress, strain, and material properties
Practice calculations: Be comfortable with beam analysis, deflection calculations, and failure theories
Study current standards: Familiarize yourself with relevant ASTM and ASCE standards
Understand modern applications: Learn about smart materials and sustainability trends

Soft Skills Development

Problem-solving approach: Demonstrate systematic thinking
Communication skills: Explain complex concepts clearly
Teamwork examples: Prepare stories showcasing collaboration
Continuous learning: Show awareness of industry trends

Free PDF Download

Get the Complete Guide: Our comprehensive PDF contains all 100 questions with detailed answers, practical examples, and additional resources for interview success.

What’s Included:

Complete Q&A compilation
Formula reference sheet
Modern testing standards overview
Industry trend analysis
Interview preparation checklist

Conclusion: Your Path to Interview Success

Mastering strength of materials interviews requires combining theoretical knowledge with awareness of current industry trends. By understanding both fundamental principles and emerging technologies, you’ll demonstrate the comprehensive expertise employers seek.

Key Takeaways:

Master fundamental concepts and their modern applications
Stay current with testing standards and emerging materials
Prepare practical examples showcasing problem-solving skills
Understand sustainability and digital transformation trends
Practice explaining complex concepts clearly

Ready to ace your next interview? Download our complete PDF guide and join thousands of successful engineers who’ve advanced their careers with our expert-curated resources.

Related Resources

In conclusion, our “Top 100 Interview Questions and Answers on the Strength of Materials” guide is your one-stop resource for mastering the concepts and techniques essential for success in materials engineering interviews. By providing you with in-depth knowledge, practical examples, and expert insights, this guide empowers you to face any interview question head-on confidently. Test yourself with Strength of Materials interview questions MCQ at the end of every section to check your understanding.

With our expert-curated compilation of essential questions and detailed answers, you’ll be well-equipped to showcase your mastery of Strength of Materials and make a lasting impression on your potential employers. Download your copy today and embark on a successful journey in materials engineering!

Remember, success in an interview is not just about showcasing your technical expertise but also demonstrating your ability to solve problems, communicate effectively, and think critically. By thoroughly preparing with our comprehensive guide, you’ll gain a solid understanding of the Strengths of Materials and develop the skills needed to excel in your future career.

Now that you’ve acquired the knowledge, it’s time to test it and make your mark in the world of materials engineering. We wish you the best of luck as you embark on this exciting journey toward professional success!

Related Posts:

FAQs

What are the questions asked in an interview about the strength of materials?

Interview questions on the strength of materials typically cover topics such as stress, strain, material properties, failure theories, and deformation. They may include questions about stress-strain diagrams, Young’s modulus, shear force, bending moment, beam deflections, column buckling, and torsion.

What are the basics of the strength of materials?

The basics of material strength involve understanding the mechanical properties and behaviors of materials under different loads. Key concepts include stress, strain, elasticity, plasticity, material properties, failure criteria, deformation, and beams, columns, and shaft analysis.

What is stress in the strength of materials?

Stress in material strength refers to the internal resistance per unit area that a material exhibits when subjected to an external force. It is typically measured in units of force per unit area, such as Pascals (Pa) or Newtons per square meter (N/m²). Different types of stress exist, including tensile, compressive, and shear stress.

What are basic mechanical interview questions?

Basic mechanical interview questions typically cover fundamental mechanics, materials, and design concepts. Examples include questions about thermodynamics, fluid mechanics, heat transfer, materials properties, stress and strain, failure theories, fatigue, and mechanical design principles. These questions are intended to gauge a candidate’s understanding of the foundational concepts in mechanical engineering.